| |
| |
铁板应力分布知识的调律理论推衍
吴红江 |
| |
|
对于西方人,一个问题倘能逻辑地解决,那是够满足的了,而中国人则不然。纵令一个问题在逻辑上是正确的,还须同时衡之以人情。确实,“近乎人情”是较胜于“合乎逻辑”的伟大考量。因为一个学理可以根本违反普通感性而却很合乎逻辑。
——林语堂 |
| |
| |
吕思清介绍国外的“名琴协会”时曾指出:国外的私人收藏家们都会把他们收藏的小提琴拿出来借给年轻的音乐家们。他们这样做有两个好处,一是小提琴只有不断被使用它的音色才会越来越美;二是很多年轻的音乐家苦于没有好琴用,严重影响了他们的个人发展,从名琴协会借琴不但能为小提琴保值,还能使音乐家们从中获益。 [ 《吕思清:名琴升值速度快 想成立名琴协会》,《北京娱乐信报》, 2007 年 03 月 25 日 ] 这段话提供了如此信息:音板需要良好振动才能保持其价值,发挥其真正功能。
什么是良好振动呢?对提琴而言,是高超演奏技术成就的精确音准及良好泛音产生的共振;对钢琴而言,是铁板应力均衡状态下的相对精确的音准关系(良好音准曲线)产生的共振。
铁板应力的分布与音板球面弧度的变化
钢琴的良好共振要以“铁板应力均衡”为前提是因为钢琴的铁板承受巨大的拉应力和压应力,应力不均衡下的相对精确的音准关系将随着铁板应力自行趋于均衡的变化趋势而失去,良好共振也将不复存在。
以竖式钢琴为例。根据《钢琴铁板应力测试与分析》(肖巍,《广东乐器世界》 2010 年 6 期),调律后,最大拉应力值和最大压应力值同时发生在同一区域。第一次调音时,最大拉应力发生在图 “竖式钢琴铁板应力承受点” 中 a 点。第二次调音时,最大拉应力发生在图中 b 点。图中 c 点高度压应力集中,接近破坏极限。根据机械设计手册,在此三点区域,如果装配(调律)不得当,即有因为超过拉应力极限而断裂的可能,又有超过压应力而损坏的危险。 |
| |
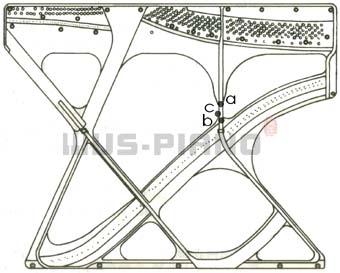
竖式钢琴铁板应力承受点
|
| |
| 而调律,特别是不规则、大幅度走律之后的调律,无疑是铁板应力的又一次分布,如果工作不当,也会有铁板损坏或断裂的可能。调律过程中,铁板所受应力随调律进程而发生变化,如果变化导致 C 点左右两侧铁板所受应力差值较大,则会对铁板造成损伤,即便当时没有显露出问题,也可能会在将来的某日发生断裂。图《应力分配不当导致大修后的钢琴铁板断裂》中的钢琴即是在大修之后 5 年时发生的铁板断裂。 |
| |

应力分配不当导致大修后的钢琴铁板断裂
|
| |
铁板应力的分布状况难以感知,其变化趋势却可以通过钢琴的音准状况加以判断,其均衡分布的状态却可通过利用与铁板密切相关的音板在调律过程中的运动趋势促成。
调律后,铁板应力的变化趋势大致是这样的:在琴弦的作用下,频率提升时,应力相对增加;频率降低时,应力相对减少。 |
| |
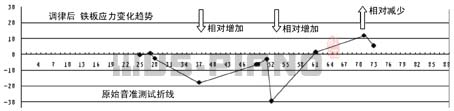
铁板应力分布变化趋势示意图
(纵坐标表示偏离音分数,横坐标表示键号。下同。)
|
| |
| 调律后,音板球面弧度的变化趋势大致是这样的:在琴弦的压应力作用下,频率提升时,音板下沉;频率降低时,音板上隆。 |
| |

音板球面弧度变化趋势示意图
|
| |
| |
铁板应力分布的相关问题
由于调律是一个持续过程,所以铁板应力的分配不是瞬间完成的。因为中音、高音分档处是应力汇集的地方,调律引起的中音区的铁板应力变化将增大或减少其与高音区铁板应力之间的差值。忽视这一现实问题,固执地按照基准音组 - 中音区 - 高音区的顺序调律,虽然因惯性工作习惯而提高工作速度,却因较大改变钢琴应力分布而影响其音准稳定,甚至对钢琴造成损伤。 |
| |
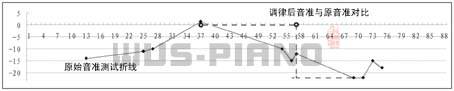
调律过程对音分差值及应力分布的影响示意图
|
| |
以《调律过程对音分差值及应力分布的影响示意图》为例: 57 键(中音、次高音分档处, -12 音分)与 69 键(次高音、高音分档处, -22 音分)在未经调试之前,各自对应的标准音高频率音分差值之间相差 10 音分,待 57 键提升至理论音高频率( 0 音分)后与未经调试的 69 键( -22 音分)各自对应的标准音高频率音分差值即增至约 22 音分。对铁板而言,铁骨两侧应力差骤增,增加了损坏的潜在因素;对调律效果而言, 22 音分的差值较 10 音分的差值音准稳定性差。
音准稳定性直接影响到以音准为基础的音板的 共振——由此可知,铁板应力分布影响音板共振。 为保护铁板、提高音准稳定性、获取音板良好共振,此例可先参照次高音区提升高音区音准,减少铁骨两侧应力差的变化——此即音区工序的设定对于铁板应力分布的影响。
音板球面弧度变化的相关问题
由于调律是一个持续过程,所以音板球面弧度的变化不是瞬间完成的,并且某一区域的音板球面弧度变化必将波及其他区域的音板并引起相应的球面弧度发生变化。
以《 音板球面弧度变化趋势示意图》所示情况为例——在分律并向高音区八度扩展调律的过程中,中音区音律提升,音板球面弧度受琴弦的压力作用 而下沉,导致音板从此处向两侧压展,两侧音板产生相对 上隆的变化趋势。此推论的前提条件是假定外壳仅产生适度相应变化。(有关外壳与音板变化相应关系的内容请参阅拙文《钢琴结构浅说》第一编《平台钢琴》第五章《外壳》 之 《独特的美森翰林声学结构》。原载《中外乐器信息》 2008 年 10 期。) 因为中音、高音分档处是应力汇集的地方, 高音区音板受中音区音板变化的影响较大。 忽视这一现实问题,固执地将标准音确定为 49A — 440Hz ,虽然暂时地在钢琴上获得了国际标准音高,却因较大变动钢琴应力分布而影音准稳定,甚至对钢琴造成损伤。 |
| |

音板球面弧度变化趋势对标准音设定的影响
|
| |
此例,比较理论频率值,该琴在 37A 键偏离 +21 音分,在中音、高音分档处偏离 +8.8 音分,在次高音、高音分档处偏离 + 20 音分。将标准音频率降低后,中音区音板因所受琴弦压应力的减少而球面呈上隆趋势、弧度增大,当将 49A 设定为 440Hz ( 37A 偏离 0 音分)时,频率降低 21 音分的幅度,将极大地影响次高音区及高音区音板,使该区域音板产生球面弧度下沉的变化趋势。最大的问题是直接影响次高音、高音分档处的相对音准关系状况,使原本尚可的相对音高 ( +21 音分: + 20 音分) 在调律后难以维持。
相对音高是铁板应力分布状况和 音板 振动状况的综合反映,相对稳定的音准与相对良好音准曲线即代表相对均衡的铁板应力分布和相对良好的 音板共 振。为了获取相对良好而稳定的曲线,此例将该琴标准音 49A 设定为 440Hz+15 音分。
理论的推衍
诚然,上述“铁板应力分布的相关问题”及“音板球面弧度变化的相关问题”内容均为本人猜想,尚无法提供算式或函数式用于推衍。
频率变化对铁板及音板的变化趋势仅可推论如下: |
| |
频率变化对铁板及音板的影响
频 率 |
拉应力 |
压应力 |
音板球面弧度变化趋势 |
增 高 |
增加 |
增加 |
下沉趋势 |
降 低 |
减少 |
减少 |
上隆趋势 |
|
| |
所幸有一些工作记录,可以作为客观事实的理论依托,摘录部分于下:
中音区分律及同八度调试前后各分档处频率值偏离音分数对比
钢琴型、序号 |
调律 |
中音、低音分档 |
标准音( 37A ) |
中音、次高音分档 |
次高音、高音分档 |
温 / 湿度 |
Kawai XO-8 2231234 |
前 |
-17 |
-15.5 |
-8.5 |
-6 |
+3 |
26.6 。 C
36-45% |
后 |
-17.7 |
—— |
-10.5 |
-4.3 |
+4.9 |
Kawai K8
2579748 |
前 |
-7.8 |
-0.7 |
+6.1 |
-2.5 |
+10.4 |
30.8 。 C
28% |
后 |
-7.8 |
—— |
+4.8 |
-9.5 |
-10.2 |
Kawai K8
2601086 |
前 |
-19.7 |
-12.7 |
1.3 |
-21 |
-11 |
27.5 。 C
43% |
后 |
-21.7 |
—— |
-0.8 |
-23.5 |
-11.6 |
Kawai K8
2578218 |
前 |
-8.8 |
-1.9 |
+3.7 |
-27.7 |
-19 |
29.7 。 C
48% |
后 |
+3 |
—— |
+2.8 |
-33.1 |
-25.4 |
Yamaha U300SX
5529565 |
前 |
-8.7 |
-14.2 |
-4.3 |
-10.7 |
-5.1 |
28.9 。 C
81% |
后 |
-9 |
—— |
-7.5 |
-9.2 |
-12.4 |
|
| |
这些数据侧面反映出在调律过程中随着调试区域琴弦应力的增加,音板弧度发生变化,导致其他区域的琴弦应力发生变化。
也许这些记录的数据没有充足到让大家感到足以彻底支撑本人的猜想,但充足的数据恰是本人有意避免的。对于音准的调试,必须在适量的精确数据之上加之合理的想象——本人称之为“模糊概念”——唯此才使得音律通于人性,悦于人耳。如此想法一如 林语堂 先生对于中国人学术的评述。
当然,表中所示的这些应力变化,甚至调律完结时的应力变化并非最终的变化——应力经过一定时间的变化才趋于稳定。试想一下走律较多的钢琴需要增补调律即可明了这种变化。调律师所要做的就是要尽量科学推测应力 - 音板变化趋势、尽量减少应力 - 音板变化范围以增加应力稳定性。
至此导出结论——相对良好而稳定的音准曲线即代表相对良好的 音板共 振和相对均衡的铁板应力分布,为获此结果,在拉应力的合理范围之内,必须以尽量小的音板球面弧度变化获取琴弦压应力的合理分布。相关实践案例请参阅拙文《铁板应力分布知识在调律实践中的应用》(原载《中外乐器信息》 2011 年 4 期)。
附:温湿度变化对标准音音高设定的影响
本人的工作区域主要在北京、天津及河北的部分城市。这一地区的气候特点是冬季相对寒冷、干燥,夏季相对炎热、潮湿。在这一区域,可以明显感到温湿度变化对钢琴音准产生的影响。以红江钢琴工作室为北京师范大学音乐系连续三年跟踪调律服务的数据为例:经过 2008 年暑假, 703 琴房室内温度 30 。 C ,湿度 48% ,钢琴珠江 118M6 — 551853 的标准音 49A 竟自升至 448Hz ;经过 2009 年寒假, 719 琴房室内温度 24.8 。 C ,湿度 17% ,钢琴珠江 118M6 — 554105 的标准音 49A 竟自降至 426Hz 。这是钢琴音板球面弧度受湿度增加的影响而上隆,造成琴弦应力增加、频率升高;钢琴音板球面弧度受湿度减少的影响而下沉,造成琴弦应力减少、频率降低的显著例子。技师对于此类钢琴,在设定标准音音高频率时,在考虑铁板应力分布状况及音板球面运动趋势的同时,要兼顾考虑到摆放环境的温湿度变化趋势。
以上述调律服务为例:按照协议,红江钢琴工作室在每年的 2 月底— 3 月初、 8 月底— 9 月初为北京师范大学音乐系提供两次调律服务。在每年春季调律时,考虑到即将进入的夏季湿度较大,钢琴音准有升高趋势,不对标准音进行过量提升;同时考虑不降低标准音以保持相对音准稳定,按照“琴房内的钢琴在 低于 438Hz 标准时,依情况将标准音设定至 438Hz 或 440Hz ,高于 440Hz 标准时标准音设定为 442Hz ” 的原则调律。 在每年 秋 季调律时,考虑到即将进入的冬季湿度较小,钢琴音准有降低趋势,考虑不降低标准音以保持相对音准稳定,按照“琴房内的钢琴在 低于 440Hz 标准时将标准音设定至 440Hz ,高于 440Hz 标准时维持原标准音高度 ”的原则调律。 |
| |
采用针对北师大环境制定的调律计划的服务效果对比
偏离音分值 |
占调律钢琴总量的百分比 |
秋季服务前原始数值的变化 |
春季服务前原始数值的变化 |
08 年 8 月 |
09 年 9 月 |
09 年 3 月 |
10 年 2 月 |
<10% |
20 |
17 |
6 |
23 |
10% — 20% |
36 |
50 |
50 |
42 |
20% — 30% |
24 |
21 |
26 |
17 |
30% — 40% |
4 |
8 |
8 |
4 |
40% — 50% |
0 |
4 |
8 |
10 |
>50% |
16 |
0 |
2 |
4 |
请注意:在秋季调律时,我们预设了约 8 音分的标准音偏差;在春季调律时,我们甚至预设了更多的标准音偏差。 |
| |
从服务结果来看,采用此标准音设定原则调律后,秋季服务前,偏离音分值小于 20% 的钢琴从 56% 增至 67% ,偏离音分值大于 20% 的钢琴从 44% 减至 33% ,特别是偏离音分值大于 50% 的钢琴从 16% 减至 0 ;春季服务前,偏离音分值小于 10% 的钢琴从 6% 增至 23% ,偏离音分值小于 20% 的钢琴从 56% 增至 65% ,偏离音分值大于 20% 的钢琴从 44% 减至 35% ,偏离音分值 20% — 40% 的钢琴从 34% 减至 21% ,仅偏离音分值大于 40% 的钢琴增加了 4% 。
可见,按此调律计划操作既减轻了相对劳动强度,又保证了相对调律效果。 |
| |
| |
| |
| 原载《中外乐器信息》2011年9期 |
|





